Hack109のブログ

プログラミングなどで学んだことを投稿していきます。

『絶対にバグらない二分探索の実装パターン』を使って競プロの問題を解く。【競技プログラミング】

はじめに

絶対にバグらない二分探索の実装パターンと豪語している記事がありました。 qiita.com

今回はこれを使って競技プログラミングの問題を解けるのかを試します。

挑戦した問題

今回挑戦した問題はABC319のD問題です。 atcoder.jp

解き方としては、答えになりうる最大値と最小値を算出し、二分探索を行う、 というものです。

そこまでは分かったのですが、いろいろ試してもサンプル含め半分くらいしか正解できません...。

問題の解説を見ても、なぜか最後に-1するのが答えとなっていたりします。汎用的な解き方ではなさそうなのであまり納得ができませんでした。 また、めぐる式二分探索という方法も使ってみましたが、結果は同じでした。

絶対にバグらない二分探索の実装パターン

そんな中、見つけたのがこの絶対にバグらない二分探索の実装パターンという記事でした。 記事をよく見ると、めぐる式二分探索と違ってコーナーケースに強いとも言っています。 qiita.com

そこまでいうならと、この実装方法を用いて、ABC319のD問題を解いてみました。 実装したソースは下記になります。

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <math.h>
#include <set>

using namespace std;
using llong = long long;

int main()
{
    int N = 0, M = 0;
    llong left = 0;
    llong right = 0;


    cin >> N >> M;


    vector<llong> L(N);

    for (int i = 0; i < N; i++)
        cin >> L[i];

    for (int i = 0; i < N; i++) {
        L[i] += 1; //L[i]の間に空白が入ることを想定
        left = max(left, L[i]);
        right += L[i];
    }

    left--; //L[i]の最大値が1行で収まった場合、最後が空白にならないので、空白の1文字分を減算
    right--; //L[i](0 <= i < N)が1行で収まった場合、最後が空白にならないので、空白の1文字分を減算

    left--; //https://qiita.com/hamko/items/794a92c456164dcc04ad　に従い、二分探索処理前にleftを1減算

    while (right - left > 1) {
        llong middle = (right + left) / 2;

        llong row = 1;
        llong col = 0;

        for (int i = 0; i < N; i++) {

            col += L[i];

            if(col > middle + 1){
                row++;
                col = L[i];
            }
        }

        if (row <= M) { //条件に収まっている場合はright=middle
            right = middle;
        }
        else {
            left = middle;
        }
    }

    cout << right << endl; //https://qiita.com/hamko/items/794a92c456164dcc04ad によれば、rightが答えになるらしい。


    return 0;
}

そして結果は...

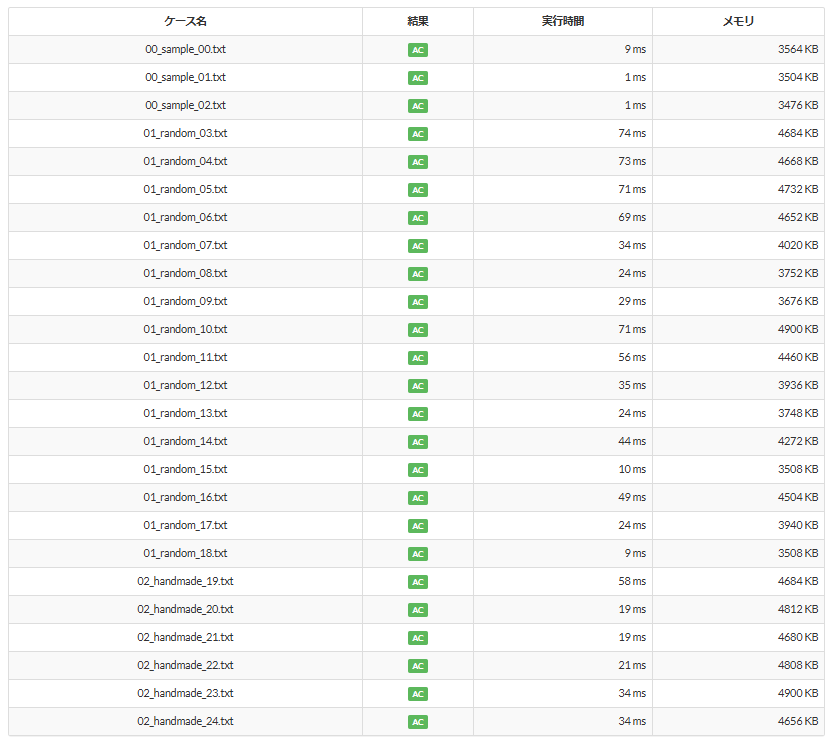
見事、すべてACにすることができました！

最後に

絶対にバグらない二分探索の実装パターンと豪語していたので、どんなものなのかと思いましたが、 言うだけあって、この方法を試すと一発で解くことができました。 他のケースにも使えるかもしれません。

hamkoさん ありがとうございました。

qiita.com

ランキング参加中
テクノロジー

ランキング参加中
AtCoder

再帰関数を活用して解く、AtCoder コンテスト過去問まとめ【競技プログラミング】

はじめに

競技プログラミングでは、再帰関数を実装して解く必要のある問題が出題されることがあります。 今回は、そのような問題をまとめてみました。 昨日参加した AtCoder Beginner Contest 378でもD問題で再帰関数を使った探索の問題が出題されましたが、たった1行、実装の仕方を間違えてしまい、 正解とはなりませんでした。(泣)

問題
1. AtCoder Beginner Contest 378 D - Count Simple Paths
2. AtCoder Beginner Contest 340 C - Divide and Divide
3. AtCoder Beginner Contest 304 D - A Piece of Cake
4. AtCoder Beginner Contest 138 D - Ki


解説の解答例では再帰関数を使ってませんでしたが、私がそれで解いた問題も含めています。見つけ次第、また更新していきます。

私事ですが、初参加から4ヵ月もかけ、ようやく茶色コーダになりました。
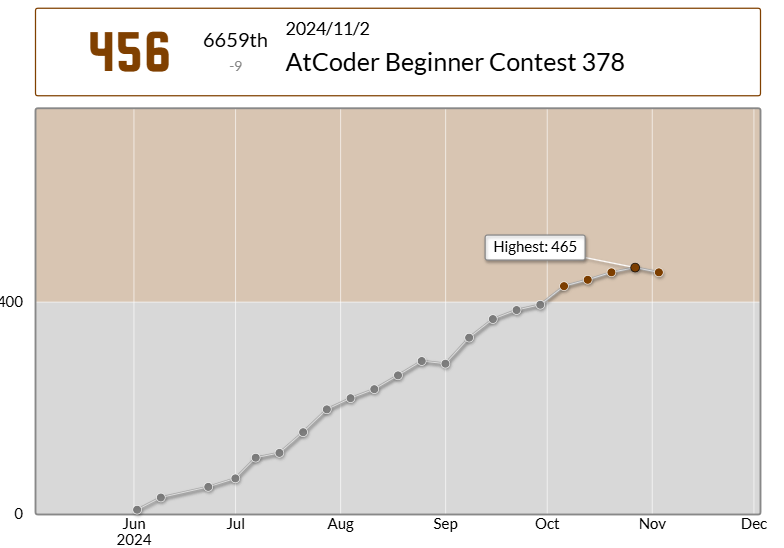
水色コーダを目指し日々精進していますが、まだまだ時間はかかりそうです。

ランキング参加中
テクノロジー

ランキング参加中
AtCoder

一次元の累積和について【競技プログラミング】

はじめに

一次元の累積和は、このような問題で使用できます。

【例題】
N日間にわたって開催された展示会について、i日目にはAi人が来場しました。 この展示会について、Q個の質問に答えるプログラムを作成してください。

  • 展示会におけるL1日目からR1日目までの総来場数は？ 　
    　 ・・・ 　
  • 展示会におけるLQ日目からRQ日目までの総来場数は？　 　

制約

  • 1 <= N <= 100000
  • 1 <= A <= 10000
  • 1 <= L <= R <= N

累積和(一次元)の使いどころ

一列に並べられた数値について、x番目からy番目に格納されている値の総数を算出するときに使用できます。

累積和(一次元)のアルゴリズム

i日間の展示会の総来場数を下記とします。
累積和のアルゴリズムをしない場合、4日目から8日目の総来場数を求める場合は、
A4+A5+A6+A7+A8 で算出されます。

例題ではQ個の質問に答えるプログラムを作成することを求められています。 質問が1つならともかく、複数の質問に答えなければならないとなると、L,R日目に入力される値によっては実行時間が大きくなります。 (1つ目の質問が1日目から17日目、2つ目の質問が2日目から16日目みたいに…)

そこで、累積和のアルゴリズムを用いて効率的に算出していきます。

累積和により、i日目の総来場数を算出する。

L日目からR日目までの総来場数を算出する前に、i日目までの累計来場者数Siをあらかじめ計算しておきます。

L日目～R日目の総来場数は..?

i日目までの累計来場者数が分かれば、L日目からR日目の総来場者数は下記の計算で算出できます。

(R日目までの累計来場者数SR) - (L-1日目までの累計来場者数SL-1)

あらかじめi日目までの累計来場者数が算出されていることで、 例題のようにL日目からR日目までの総来場者数をQ個質問されていても、 総来場者数の計算は一度の計算で済みます。

#include <iostream>
#include <vector>

using namespace std;

int main() {

    int N = 0;
    int Q = 0;


    cin >> N >> Q;


    int offset = 1;
    vector<int> A(N + offset, 0);
    vector<int> S(N + offset, 0);
    vector<int> L(Q + offset, 0);
    vector<int> R(Q + offset, 0);

    for (int i = 1; i <= N; i++) cin >> A[i];
    for (int j = 1; j <= Q; j++) cin >> L[j] >> R[j];

    for (int i = 1; i <= N; i++) S[i] = S[i - 1] + A[i];

    for (int j = 1; j <= Q; j++) {
        cout << S[R[j]] - S[L[j] - 1] << endl;
    }

    return 0;
}

さいごに

まとめ

一次元の累積和のアルゴリズムは、一列に並べられた数値について、x番目からy番目に格納されている値の総数を算出するときに使用できます。

ランキング参加中
テクノロジー

二分探索について【競技プログラミング】

はじめに

二分探索は、探索範囲を半分ずつ絞りながら正解データを特定するアルゴリズムです。 下記のような問題に使用できます。　
　
【例題】　 小さい順に並べられているN個のデータA=[A1 ～AN]があります。要素XはAの何番目に存在するかを出力してください。　
　
全探索でも解けますが、二分探索で実装してみます。 こちらが二分探索を用いた解法です。

#include <iostream>
#include <vector>

using namespace std;


int BinarySearch(vector<int> a, int x, int n) {

    int L = 1;
    int R = n;
    int M = 0;

    while (L <= R) {

        M = (L + R) / 2;

        if (a[M] == x)
            return M;

        if (a[M] < x)
            L = M + 1;

        if (a[M] > x)
            R = M - 1;
    }

    return NULL;
}

int main(){

    int N = 0;
    int X = 0;
    int ans = 0;


    cin >> N >> X;

    int offset = 1;
    vector<int> A(N + offset, 0);

    for (int i = 1; i <= N; i++)
        cin >> A[i];

    ans = BinarySearch(A, X, N);

    if (ans == NULL)
        cout << "No" << endl;
    else
        cout << ans << endl;

    return 0;
}

　

二分探索が可能となる条件

二分探索を行うための条件は下記です。　
　
・配列が小さい順になっている。　
　
そのため、小さい順になっていない配列に対して二分探索を行う場合は、配列を小さい順に整列するソートを行う必要があります。 　

二分探索のアルゴリズム

探索範囲を半減させる。

配列の中央にあたる値と探索している値の大小関係を確認し、探索範囲を半減させていきます。 要素数17の配列から19を探索する流れを下記に示します。 1巡目では、インデックス番号9が真ん中の中央にあたるため、そこに格納されている値と探索している値の大小関係を比較します。結果、探索している値のほうが小さいので、インデックス番号1～8のどこかに格納されていることがわかります。 2巡目、3巡目でも同じ処理を行い、探索範囲を半分に絞り続けます。 4巡目の探索で、配列の5番目に19が格納されていることがわかりました。

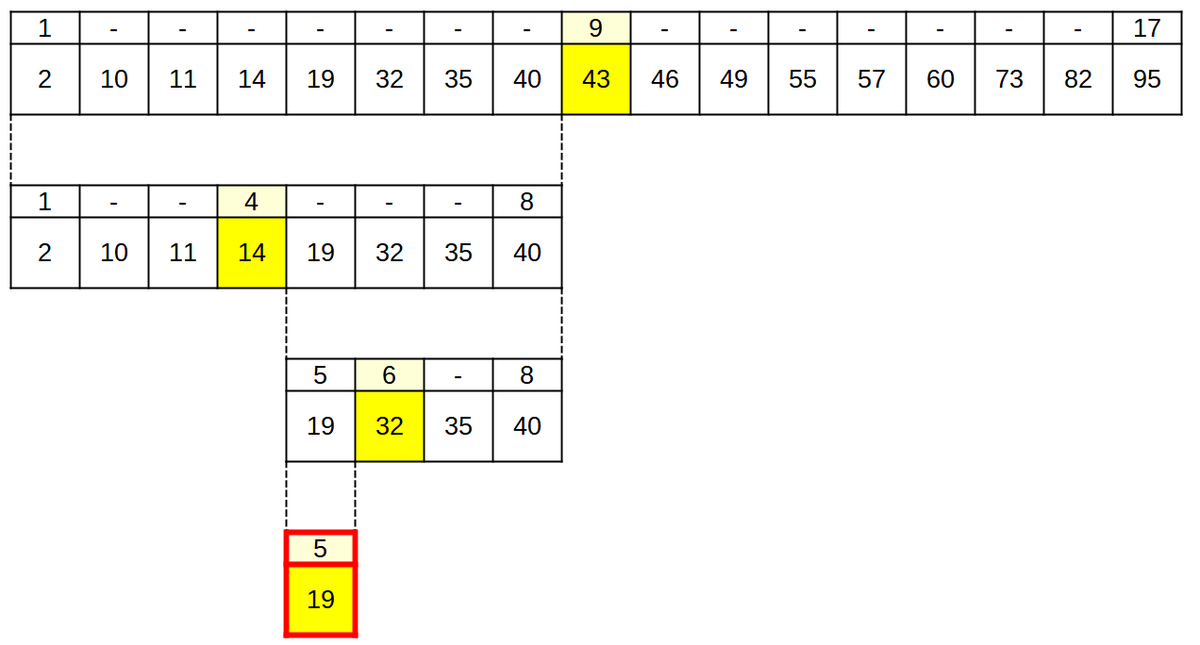
49を探索した場合を下記に示します。探索範囲の中央の値が探索している値だった場合、その時点で探索完了となります。

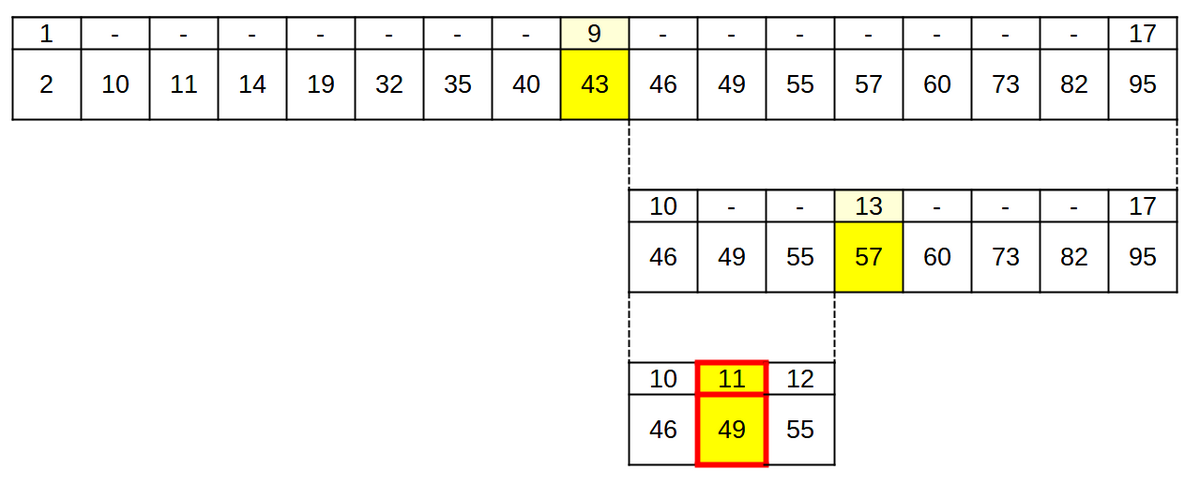
二分探索を実装する。

二分探索を実装していきます。例題を再度提示します。

【例題】 小さい順に並べられているN個のデータA=[A1 ～AN]があります。要素XはAの何番目に存在するかを出力してください。 　
データ数N, 探索したい値X, 配列の値Aを入力していきます。

    int N = 0;
    int X = 0;
    int ans = 0;


    cin >> N >> X;

    int offset = 1;
    vector<int> A(N + offset, 0);

    for (int i = 1; i <= N; i++)
        cin >> A[i];

　
入力した値を、二分探索を行う関数に引数として渡します。

 ans = BinarySearch(A, X, N);

　
二分探索の関数の中身です。L,R,Mはインデックス番号の値が格納されます。　
L:探索範囲のインデックス番号　最小値　
R:探索範囲のインデックス番号　最大値　
M:探索範囲のインデックス番号 　中央値　

int BinarySearch(vector<int> a, int x, int n) {

    int L = 1;
    int R = n;
    int M = 0;

    while (L <= R) {

        M = (L + R) / 2;

        if (a[M] == x)
            return M;

        if (a[M] < x)
            L = M + 1;

        if (a[M] > x)
            R = M - 1;
    }

    return NULL;
}

　
中央値については、 M = (L + R)/2 で算出されます。探索範囲のデータ数が偶数だった場合、中央値の算出は切り捨てになります。 値が見つかればMの値を返します。 値が見つからなかった場合、Lの値がRを上回るため、ループから抜けるかたちとなり、NULL値を返します。

 while (L <= R) {

        M = (L + R) / 2;

        if (a[M] == x)
            return M;

        if (a[M] < x)
            L = M + 1;

        if (a[M] > x)
            R = M - 1;
    }

    return NULL;

　
探索完了後の処理です。探索していた値が見つからなければNoを出力します。

 ans = BinarySearch(A, X, N);

    if (ans == NULL)
        cout << "No" << endl;
    else
        cout << ans << endl;

　
全体のコードは以下です。

#include <iostream>
#include <vector>

using namespace std;


int BinarySearch(vector<int> a, int x, int n) {

    int L = 1;
    int R = n;
    int M = 0;

    while (L <= R) {

        M = (L + R) / 2;

        if (a[M] == x)
            return M;

        if (a[M] < x)
            L = M + 1;

        if (a[M] > x)
            R = M - 1;
    }

    return NULL;
}

int main(){

    int N = 0;
    int X = 0;
    int ans = 0;


    cin >> N >> X;

    int offset = 1;
    vector<int> A(N + offset, 0);

    for (int i = 1; i <= N; i++)
        cin >> A[i];

    ans = BinarySearch(A, X, N);

    if (ans == NULL)
        cout << "No" << endl;
    else
        cout << ans << endl;

    return 0;
}

　

二分探索の応用例

二分探索の応用例です。

単調増加の関数

【例題】 正の整数Nが与えられます。N=x3を満たす正の実数xを出力してください。ただし、絶対誤差が0.001以下であれば正解とします。 　
　
探索対象のデータが他の要素に対して強い正の相関関係であれば、二分探索を用いることで正解データを特定できます。

#include <iostream>

using namespace std;

double Function(double x) {
    return x * x * x;
}

int main(){

    double N = 0;

    double x_H = 1000000000;
    double x_L = 0;
    double x_M = 0;
    double answer = 0;

    cin >> N;

    while (x_L < x_H) {

        x_M = (x_L + x_H) / 2;
        answer = Function(x_M);

        if (answer >= (N - 0.001) && answer <= (N + 0.001)) {

            cout << x_M << endl;
            break;
        }

        if (answer < N)
            x_L = x_M;
        if (answer > N)
            x_H = x_M;
    }

    return 0;
}

　

まとめ

二分探索は、探索範囲を半分ずつ絞りながら正解データを特定するアルゴリズムです。 条件として、小さい順に並べられているデータが必要になります。 そのため応用例として、探索対象のデータが他の要素に対して強い正の相関関係であれば、二分探索を用いることで正解データを特定できます。

ランキング参加中
テクノロジー

bit全探索について【競技プログラミング】

はじめに

bit全探索は、bit演算を使った全探索アルゴリズムの一種です。 部分和問題に応用できます。 例としては、下記のような問題です。

【例題】 N枚のカードがあり、カードA1 ～ANにそれぞれ異なる値段がつけられています。購入するカードをいくつか選んだ場合、購入金額がS円となる組み合わせは存在しますか？

bit全探索を用いた解法です。

#include <iostream>
#include <vector>

using namespace std;

int main(){

    int N = 0;
    int S = 0;

    cin >> N;
    cin >> S;


    vector<int> A(N, 0);

    for (int i = 0; i < N; i++)
        cin >> A[i];

    int sum = 0;
    bool answer = false;

    for (int pattern = 0; pattern < (1 << N); pattern++) {

        sum = 0;
        
        for (int bit = 0; bit < N; bit++) {

            if (pattern & (1 << bit)) {
                sum += A[bit];
            }
        }

        if (sum == S) {
            answer = true;
            break;
        }
    }

    if (answer == true)
        cout << "Yes" << endl;
    else
        cout << "No" << endl;

    return 0;
}

bit全探索のアルゴリズム

2進数表記による各組み合わせの導出

bit全探索のアルゴリズムでは2進数を用います。

桁数をデータ数とするため、データ数をNとすると組み合わせの総数は2Nとなります。 N=3の場合は、8つの組み合わせを0～7と表します。 さらに、0～7を2進数表記することで、1となっている桁を選択したデータと考えることができます。

カードAの値段それぞれをA1=30円,A2=40円,A3=20円とし、購入金額Sが50円となる組み合わせを見つける場合、購入金額がSとなる組み合わせが見つかるまで0から一つずつ確認していくことになります。この場合は6つ目の組み合わせで見つかりました。

bit全探索の実装

bit全探索を実装していきます。例題を再度提示します。

【例題】 N枚のカードがあり、カードA1 ～ANにそれぞれ異なる値段がつけられています。購入するカードをいくつか選んだ場合、購入金額がS円となる組み合わせは存在しますか？

　
まずは、カードの枚数N、購入金額S、カードのそれぞれの値段A1 ～ANを入力していきます。

    int N = 0;
    int S = 0;

    cin >> N;
    cin >> S;


    vector<int> A(N, 0);

    for (int i = 0; i < N; i++)
        cin >> A[i];

　
入力後、bit全探索の処理に入っていきます。全探索の基本的な処理は下記のとおりです。

    int sum = 0;
    bool answer = false;

    for (int pattern = 0; pattern < (1 << N); pattern++) {

        sum = 0;
        
        for (int bit = 0; bit < N; bit++) {


            if (pattern & (1 << bit)) {
                sum += A[bit];
            }
        }


        if (sum == S) {
            answer = true;
            break;
        }
    }

各組み合わせごとの購入金額をsum, 判定結果をanswerとして初期化します。

    int sum = 0;
    bool answer = false;

bit全探索では、選択肢の数に基づいて総組み合わせ数を算出する必要がありますが、シフト演算子<<を使用することで簡単に算出することができます。<<は左シフトで、2進数であらわされたデータを指定した分、左にシフトします。

カードAが3枚の場合は、3桁の2進数で表すことができる数値は0～7、つまり総組み合わせ数は8であり、1 << 3に一致します。 よって、N枚のカードから購入するカードを選択する場合、総組み合わせ数は 1 << Nで表すことができます。 forを使うことで、N枚のカードから選択する場合の組み合わせを一つずつ確認できます。patternが各組み合わせを示す数値となります。

    for (int pattern = 0; pattern < (1 << N); pattern++) {

        //各組み合わせを確認
    }

各組み合わせの購入金額を算出します。 まず、組み合わせを示す数値patternに対して、2進数で表記した場合に「1」となっている桁を探します。「1」となっている桁が見つかった場合、その桁に対応するデータを持ってきて加算処理を行っています。 この処理によって、sumに各組み合わせの購入金額が算出されます。

    sum = 0;
        
    for (int bit = 0; bit < N; bit++) {


        if (pattern & (1 << bit)) {
            sum += A[bit];
        }
    }

算出された購入金額がSと一致した場合、判定結果をtrueとし、ループ分を抜けます。

    if (sum == S) {
        answer = true;
        break;
    }

最後に判定結果を出力します。

    if (answer == true)
        cout << "Yes" << endl;
    else
        cout << "No" << endl;

全体のコードは以下です。

#include <iostream>
#include <vector>

using namespace std;

int main(){

    int N = 0;
    int S = 0;

    cin >> N;
    cin >> S;


    vector<int> A(N, 0);

    for (int i = 0; i < N; i++)
        cin >> A[i];

    int sum = 0;
    bool answer = false;

    for (int pattern = 0; pattern < (1 << N); pattern++) {

        sum = 0;
        
        for (int bit = 0; bit < N; bit++) {

            if (pattern & (1 << bit)) {
                sum += A[bit];
            }
        }

        if (sum == S) {
            answer = true;
            break;
        }
    }

    if (answer == true)
        cout << "Yes" << endl;
    else
        cout << "No" << endl;

    return 0;
}

まとめ

　bit全探索により、N個のものに対して「選ぶ」「選ばない」、「買う」「買わない」といった選択をした場合の探索を行うことができます。(部分和問題)

N個から選択する場合の総組み合わせ数は2N通りあります。

N個から選択する場合の組み合わせを2進数のN桁の値で表すことで、「選ぶ」「選ばない」を「１」「０」と考えることができます。

ルータのルーティング,ネットワーク構成を関西の駅や路線で例えて考える話

 



はじめに

ここ最近で、VPNルータを使ったルーティングの動作を確認していますが、ルータの経路情報とかネットワーク構成とか、何か身近なものに例えられないかと考えました。

ネットワーク構成図

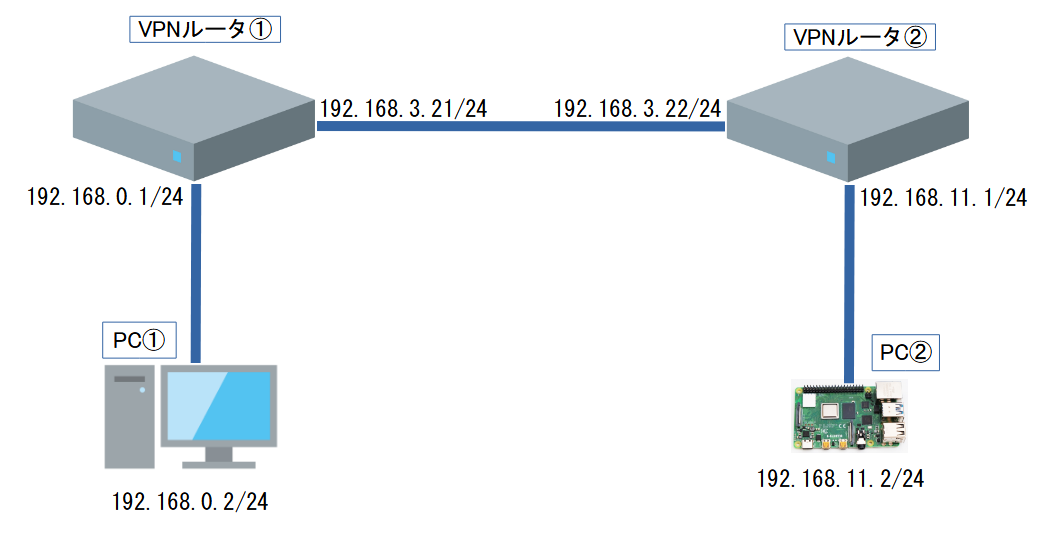
前回、スタティックルーティングを実施したときのネットワーク構成図をもとに、考えてみます。

 

hack109.hatenablog.com

ネットワーク構成 経路情報を身近なもので例えると...

ネットワーク構成の例え

ネットワーク構成の例えとして、ぱっと浮かんだのは駅や路線です。

大阪環状線

各機器をそれぞれ下記のように考えてみます。

PCやVPNルータは駅として例えられます。違いとしては、VPNルータは乗り換えのある駅で、PCは特に乗り換えのない駅です。

ネットワークは路線として考えられます。ネットワーク全体のアドレスを指すネットワークアドレスを京阪線、JR線などの路線として考えることで、そのネットワークに属しているルータやPCを駅として考えられます。

 

VPNルータ　　　　　　　

駅 (乗り換えあり)　　　　　　　　　

PC　　　　　　　　

駅 (乗り換えなし)　　　　　

ネットワーク　　　　

路線　　　　　　　　　　

 

経路情報の例え

ルータが持っている経路情報を何かに例えるとなると、駅員さんの路線に関する知識や路線図がそれにあたると思います。

駅員さん

経路情報は、VPNルータが記憶している目標の機器にデータを送るための経路になります。

電車で例えると、目標の駅までにいくには次にどの路線に乗り換える必要があるのかという情報を記憶している必要があるわけです。

駅を利用する客(データ)がどの路線に乗り換えるのかを把握していなくても、路線図を見たり駅員さんに聞いたりすることで、次に乗る路線が分かるわけです。

 

経路情報

駅員さんの路線に関する知識

乗客

通信データ

 

関西の駅や路線でネットワーク構成図を作る。

では、実際の駅や路線で例えて、ネットワーク構成図を作ってみたいと思います。

今回は関西の路線で考えてみます。

 

スタート,目標の駅はこちらです。

スタート　　　　　　

大阪　岸和田駅 (南海線)

目的地　　　　　　　

京都　出町柳駅 (京阪線)

 

目的地までの乗り換えの方法はいろいろありますが、今回はこちらで考えます。多分この例がわかりやすいです。

乗り換え

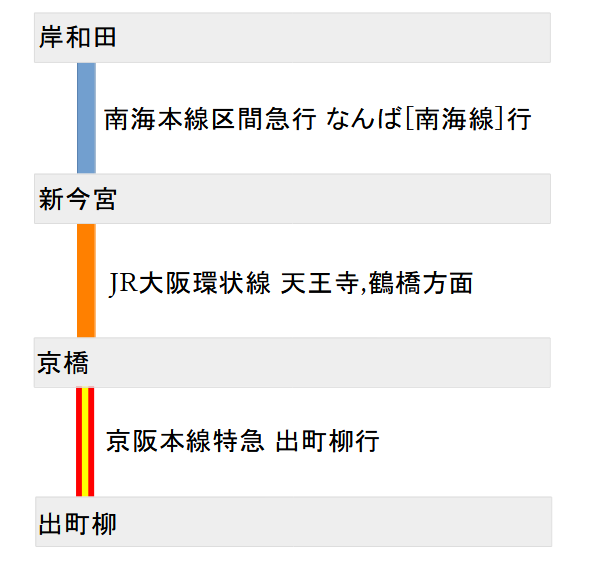
では、ネットワーク構成図に落とし込んでみましょう。

駅や路線を例として考えるネットワーク構成図

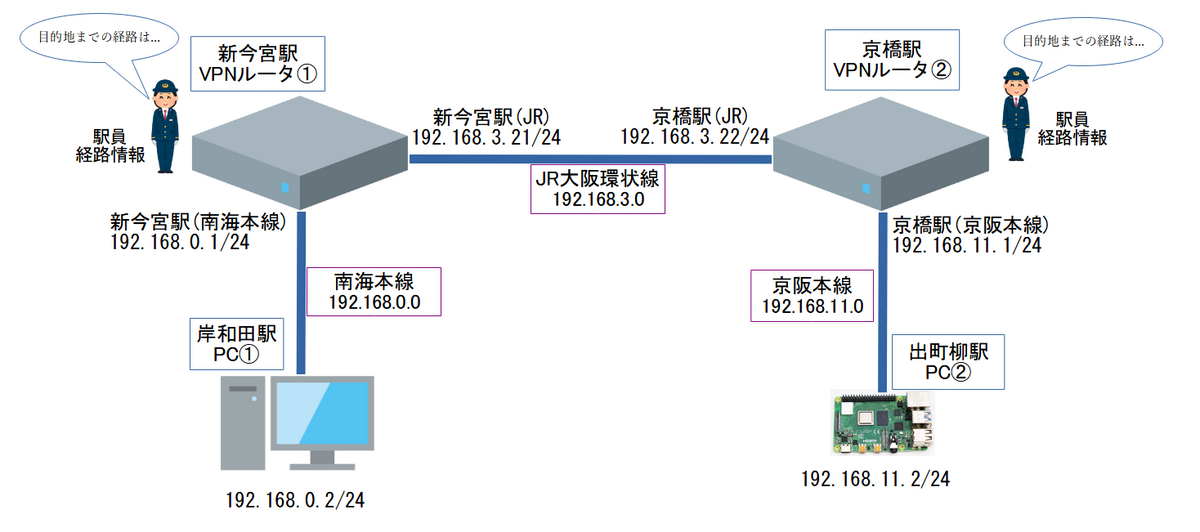
イメージしやすくなったかなと思います。駅名は同じでも、どの路線の駅かでどこに行けるかが変わります。ルータを経由して別のネットワークに転送されるところを、その部分でうまく例えられました。このように見てみると面白いですね。

 

最後に

まとめ

　今回はルータのルーティングについて、実際の路線や駅に例えて考えてみました。ここまでの記事を読んで、全体の路線図みればどこへでも行けるだろうとか、スタート地点の駅に関西の路線を把握している駅員さんもいるのではといった意見があるかもしれませんが、そこはまあ...あくまでイメージとして。

　プログラミングとかも、変数のアドレスの話が出てきたときに、家の住所を変数のアドレスと例えて説明している記事や参考書が見られます。難しそうな話が出てきたとき、身近なもので例えて自分なりに解釈することができれば、イメージしやすくなりますし、理解が深まると思います。

素材

イラストAC

無料イラスト・フリー素材なら「イラストAC」 (ac-illust.com)

いらすとや

かわいいフリー素材集 いらすとや (irasutoya.com)

 

ランキング参加中
テクノロジー

TP-Link ER605でスタティックルーティングを体験してみた。

はじめに

前回は、1つのルータを使ってルーティングを体験しました。

hack109.hatenablog.com

 

1つのルータに接続されている隣のネットワークに接続する際は、ルータに対してVLANの設定を実施すれば、直接接続のルート情報は自動的にルーティングテーブル(経路情報)に登録されていました。

しかし、ルータを2つ使用し、接続されている隣のルータで管理しているネットワークに接続するためには、

目標のネットワークへの経路情報をルーティングテーブルに追加する必要があります。

ネットワーク構成の変更が発生するたびに、ルータのルーティングテーブルを手動で修正する方法をスタティックルーティングと呼びます。

そこで今回は、実際にルータを2つ使用し、スタティックルーティングを行うことで隣のルータのネットワークに接続できるかを確認してみたいと思います。

 

目標

  • ルータを2つ使用し、スタティックルーティングを行うことで隣のルータのネットワークに接続できるかを確認する。
  • スタティックルーティングの方法を学ぶ。

使用機器・ネットワーク構成

 

ゲートウェイとして使用する機器

tp-link ER605をゲートウェイとして使用します。今回は2つ使用します。

ゲートウェイとして使用する機器

各ネットワークで使用する機器

カテゴリ

機種名

IPアドレス

PC①

DESKTOP-FLK5IJ4(OS:Windows)

192.168.0.2/24

PC②

Raspberry pi

192.168.11.2/24

 

ネットワーク構成図

ルータ同士を接続し、各ルータにPCを接続します。PC①,PC②が双方にping通信できることを確認します。

ネットワーク構成図

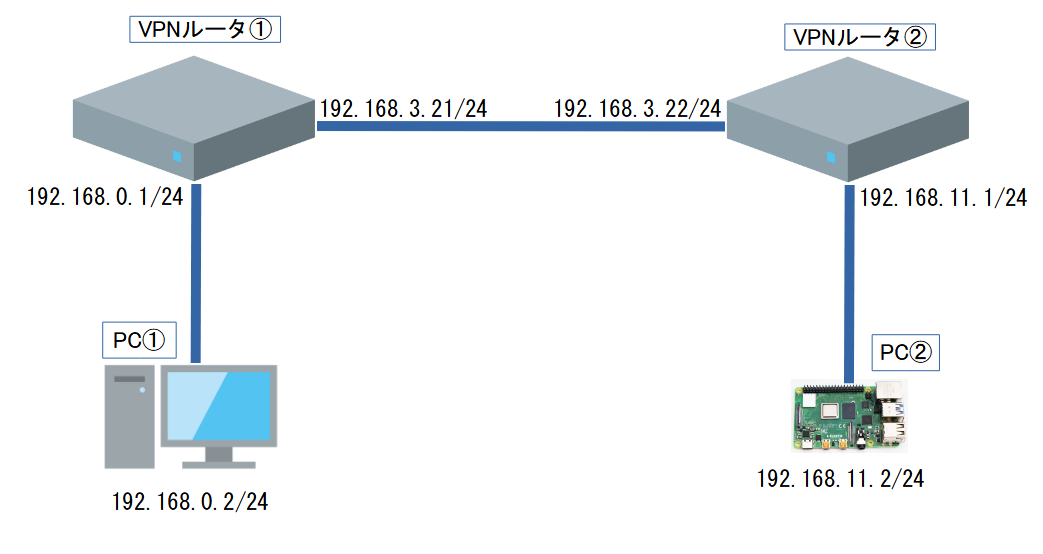
スタティックルーティング 設定方法

※著作権の問題があるため、スクショなしで説明いたします。ご了承ください。

 

隣のルータとのネットワークを構成するためには、各ルータが同じネットワークに属している必要があります。今回の例では、192.168.3.0のネットワークが該当します。

隣のルータとの接続

VLAN設定

各ルータのVLANの設定を確認していきます。PCに接続するポートについてはDHCPは有効無効のどちらでも問題ありません。ルータ同士を接続するネットワークについてはDHCPは不要のため、無効としておきます。PC②のルータ同士の接続に使用するポートがVlan3となっていますが、特に影響はありません。

 

・PC①側のLAN設定

ID

Name

Vlan

IP Address

Subnet Mask

DHCP Server

DHCP Relay

1

ToRouter

2

192.168.3.21

255.255.255.0

Disabled

Disabled

2

LAN

1

192.168.0.1

255.255.255.0

Enabled

Disabled

 

・PC①側のVLAN設定

ID

VLAN ID

Name

Ports

Description

1

1

vlan1

2(UNTAG)

LAN1

2

2

vlan2

4(UNTAG)

ToRouter

 

 

・PC②側のLAN設定

ID

Name

Vlan

IP Address

Subnet Mask

DHCP Server

DHCP Relay

1

ToRouter

3

192.168.3.22

255.255.255.0

Disabled

Disabled

2

LAN

1

192.168.11.1

255.255.255.0

Enabled

Disabled

 

・PC②側のVLAN設定

ID

VLAN ID

Name

Ports

Description

1

1

vlan1

2(UNTAG)

LAN1

2

3

vlan3

4(UNTAG)

ToRouter

スタティックルーティング 設定前 動作確認

スタティックルーティング設定前の動作を確認してみます。ルータに直接接続されているネットワークと違い、別のルータのネットワークに接続するには、VLANの設定だけではつながりません。

 

PC①→PC② ping通信

C:>ping 192.168.11.2

 

192.168.11.2 に ping を送信しています 32 バイトのデータ:

要求がタイムアウトしました。

要求がタイムアウトしました。

要求がタイムアウトしました。

要求がタイムアウトしました。

 

192.168.11.2 の ping 統計:

パケット数: 送信 = 4、受信 = 0、損失 = 4 (100% の損失)、

 

PC②→PC① ping通信

$ ping 192.168.0.2
PING 192.168.0.2 (192.168.0.2) 56(84) bytes of data.
From 169.254.11.21 icmp_seq=1 Destination Net Unreachable
From 169.254.11.21 icmp_seq=2 Destination Net Unreachable
From 169.254.11.21 icmp_seq=3 Destination Net Unreachable
From 169.254.11.21 icmp_seq=4 Destination Net Unreachable

スタティックルーティング 設定手順

スタティックルーティングを行っていきます。

 

まず、下記の手順でスタティックルーティングを行う画面に移行します。

①メニューより、Transmission→Routingを選択

②Static Routeタブを選択

 

次に設定を行います。

結論から話しますと、各ルータで下記のように設定します。

VPNルータ①

ID

Name

Destination IP

Subnet Mask

Next Hop

Interface

Metric

Status

1

Routing

192.168.11.0

255.255.255.0

192.168.3.22

ToRouter

0

Enabled

 

VPNルータ②

ID

Name

Destination IP

Subnet Mask

Next Hop

Interface

Metric

Status

1

Routing

192.168.0.0

255.255.255.0

192.168.3.21

ToRouter

0

Enabled

ネットワーク構成図

一つずつ意味を確認していきます。

このうち、特に重要になるのはDestination IPとNext Hopになります。

Name

経路の名称

Destination IP

目標となるネットワークアドレス

Subnet Mask

サブネットマスク。ネットワーク部とホスト部を識別する。

Next Hop

目標のネットワークアドレスに接続するために経由しなければならないルータのIPアドレス

Interface

他のルータを経由するときに使用する自分のルータのLANポートの名称(VLANの設定参照)

Metric

ルータの優先度であり、値が小さいほど優先度が高くなる。(0推奨)

Status

Enabled:有効

Disable:無効

 

VPNルータ①を例に説明します。

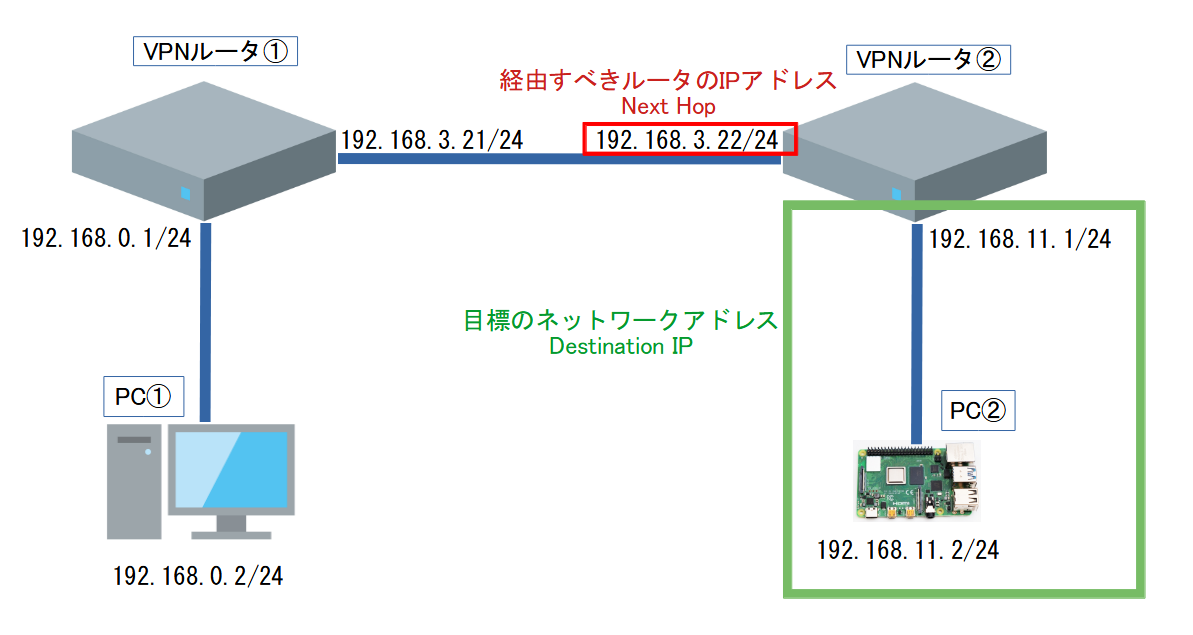
Destination IPでは、目標となる機器が属しているネットワークのネットワークアドレスを設定します。

PC①から見ると、PC②(192.168.11.2)と通信したいため、PC②が属しているネットワークアドレスである「192.168.11.0」を設定します。　

　Next Hopでは、目標のネットワークアドレスに行くために経由しなければならないルータのIPアドレスを設定します。VPNルータ①からみてPC➁にデータを送信するには、まずはVPNルータ②を経由する必要があります。そのため、VPNルータ①をVPNルータ②と同じネットワークに接続し、「PC②にデータを送信するためにはまずVPNルータ②のアドレスにデータを送信する。」と 経路を記憶させる必要があります。VPN①からみてVPNルータ②のアドレスは192.168.3.22になるため、そのアドレスをNext Hopに設定します。

これらの設定を行うことでVPNルータ①は、PC②を目標とした場合の経路情報を覚えることができます。

VPNルータ①におけるDestination IP, Next Hop

ルーティングテーブルを確認してみます。

①Routing Tableタブを選択

②Refreshをクリック

 

スタティックルーティングで設定された経路情報が追加されていることが分かります。

どちらかのルータの設定が欠けていると相互に通信ができません。

 

VPNルータ①のルーティングテーブル

ID

Destination IP

Subnet Mask

Next Hop

Interface

Metric

1

192.168.11.0

255.255.255.0

192.168.3.22

ToRouter

0

2

127.0.0.0

255.255.255.0

0.0.0.0

lo

0

3

192.168.0.0

255.255.255.0

0.0.0.0

LAN

0

4

192.168.3.0

255.255.255.0

0.0.0.0

ToRouter

0

 

 

VPNルータ②のルーティングテーブル

ID

Destination IP

Subnet Mask

Next Hop

Interface

Metric

1

192.168.0.0

255.255.255.0

192.168.3.21

ToRouter

0

2

127.0.0.0

255.255.255.0

0.0.0.0

lo

0

3

192.168.3.0

255.255.255.0

0.0.0.0

ToRouter

0

4

192.168.0.0

255.255.255.0

0.0.0.0

LAN

0

 

スタティックルーティング 設定後 動作確認

ルーティングテーブルを設定し終えたところで、再度結果を確認してみます。

ping通信にて問題なく応答されていることを確認しました。

 

PC①→PC② ping通信

C:>ping 192.168.11.2

192.168.11.2 に ping を送信しています 32 バイトのデータ:
192.168.11.2 からの応答: バイト数 =32 時間 =2ms TTL=62
192.168.11.2 からの応答: バイト数 =32 時間 =2ms TTL=62
192.168.11.2 からの応答: バイト数 =32 時間 =2ms TTL=62
192.168.11.2 からの応答: バイト数 =32 時間 =2ms TTL=62

192.168.11.2 の ping 統計:
    パケット数: 送信 = 4、受信 = 4、損失 = 0 (0% の損失)、
ラウンド トリップの概算時間 (ミリ秒):
    最小 = 2ms、最大 = 2ms、平均 = 2ms

 

PC②→PC① ping通信

$ ping 192.168.0.2
PING 192.168.0.2 (192.168.0.2) 56(84) bytes of data.
64 bytes from 192.168.0.2: icmp_seq=1 ttl=126 time=2.31 ms
64 bytes from 192.168.0.2: icmp_seq=2 ttl=126 time=2.30 ms
64 bytes from 192.168.0.2: icmp_seq=3 ttl=126 time=2.37 ms
64 bytes from 192.168.0.2: icmp_seq=4 ttl=126 time=2.42 ms
64 bytes from 192.168.0.2: icmp_seq=5 ttl=126 time=2.32 ms
64 bytes from 192.168.0.2: icmp_seq=6 ttl=126 time=2.38 ms

 

さいごに

まとめ

今回はスタティックルーティングの動作を確認しました。成功してみると設定自体はあまり難しくないですが、私は結構苦戦しました。というのも、設定はあっているのにLANケーブルをさす場所を間違えており、Ping通信がうまくいかず、解決に時間がかかりました。。。うまくいかない場合、ハード側で問題ないかを確認するくせを付けておく必要があると思います。

今後

Windows PC側でroute addで経路情報を追加し、ルータに接続された機器と通信を行う...的なやつをやってみたいです。

素材

イラストAC

無料イラスト・フリー素材なら「イラストAC」 (ac-illust.com)

 

ランキング参加中
テクノロジー